In the white flag approach, we apply ledger state changes by traversing the past cone of a milestone in a deterministic order and then applying the corresponding ledger state changes in that same order. Conflicts or invalid transactions are ignored but stay in the tangle.
Since the tangle can now contain conflicts, we can only apply the correct changes, if we start with the correct initial state.
Node operators usually use snapshot files to bootstrap their nodes. Since snapshots are simple text files containing an exported version of the ledger state, it would be very easy for an attacker to modify these files. Anybody who starts his node with such a modified snapshot file, would track a completely different version of the tangle.
We therefore need a way to “encode” the ledger state in the milestone, so that anybody who would use a tampered snapshot, could detect a divergence from the official state as soon as it happens.
One idea was, to include the root of a merkle tree in the milestone, that encodes the “applied” transactions and the corresponding ledger state, which can then be checked by the nodes before applying the changes locally.
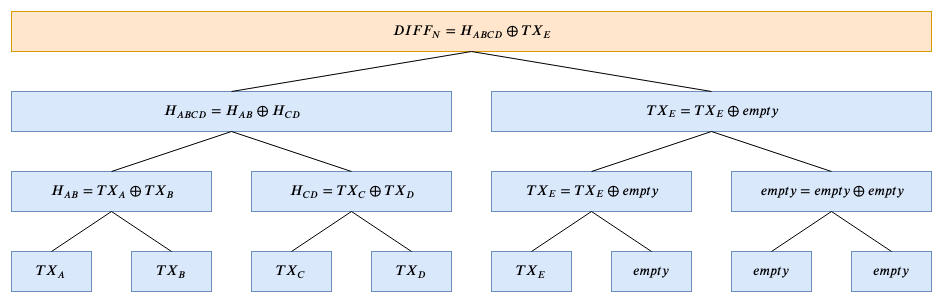
I propose to use a sparse merkle tree that uses bitwise XOR operations to combine the applied tx hashes into a merkle tree like structure to calculate a DIFF_N (where N is the number of the milestone), that encodes the list of transaction, that were applied by this milestone.
This DIFF_N hash of the changes can now be used, to encode the whole state of the ledger STATE_N by combining it with the state of the previous milestone in the following way:
This STATE_N can now be published in the milestone and used by the nodes to verify that the transactions they would apply based on their ledger state, are indeed the same ones as intended by the milestone (by doing the same calculations and then compare the locally computed STATE_N with the published one.
Using XOR when constructing the merkle tree instead of a normal hash operation, gives us several benefits:
-
It is much faster!
-
We can make the tree sparse, which means that if we have less than 2^x applied transactions, then we can simply skip calculating the hashes for the missing leaves.
This is due to two features of the XOR operation:
-
A \oplus A = empty (and therefore empty \oplus empty = empty)
-
A \oplus empty = A
which allows us to compress the calculations at the end (see example picture).
Note: It (using XOR) comes with the trade-off of loosing information about the order of the leaves but since we already have the order encoded in the tangle structure, this seems to be fine.
-
Then we wouldn’t even need the combination with the previous state, but only the DIFF.