Introduction
State of the art
In the current IOTA network, when a user wants to issue a new transaction, it must perform a certain Proof of Work (PoW) (alternatively, the user can ask - and potentially pay - a third-party service to perform the PoW). In the mainnet, the difficulty of the PoW is set to 14 (recall that every increase of this number triples the computation difficulty). Received transactions are stored in a queue and processed in FIFO order. The protocol dictates that the nodes only forward transactions if and only if the difficulty of the PoW performed is greater or equal to 14. Otherwise, transactions will be dropped.
Problems with the current implementation
The current implementation does not adapt to the varying traffic conditions, leading to either network under utilization or congestion. Furthermore, specialized hardware (e.g., FPGA) can solve the puzzle much faster than laptops or other IoT devices. To sum up, the current implementation is exposed to two fundamental problems:
-
Network congestion. In most networks, there are circumstances where the incoming traffic load is larger than what the network can handle. If nothing is done to adapt to the varying entrance of traffic, bottlenecks can slow down the entire network.
-
Spam attacks. Users having specialized hardware can solve the PoW much faster than others. This gives the opportunity to issue a very large number of transactions in short time, which could harm the network.
In the following section, we propose an algorithm based on the adaptive PoW idea [vigneri2019] which aims to mitigate the aforementioned issues.
Adaptive Proof of Work
Goal
In this article, we propose an algorithm to set a maximum allowed throughput per node. A fundamental requirement is that such a bound must be independent on the computational capabilities of a specific node. In other terms, specialized hardware cannot be exploited in order to achieve a higher throughput.
Algorithm
All nodes in the network have knowledge of three global parameters:
- Base difficulty d_0. It sets the minimum difficulty of PoW. We expect this parameter to be d_0\leq 14
- Adaptation rate \gamma\in [0, 1]. It provides the rate at which difficulty will be adjusted.
- Time window W>0. This parameter defines the granularity of the algorithm, and its role will be clarified below.
Similarly to the current implementation, issuing a new transaction must be preceded by the computation of some PoW. At time t, node i must perform a PoW with difficulty d_i(t) which can be calculated by
[Eq.1] d_i(t) = d_0 + \left \lfloor{\gamma\cdot a_i(t)}\right \rfloor,
where a_i(t) represents the number of transactions issued by node i in the time interval [t, t-W]. Note that when \gamma=0, the algorithm becomes equivalent to the current IOTA implementation.
Again, received transactions are processed in FIFO order. Let us assume we receive a transaction with difficulty d_n signed by node n. To decide whether this transaction should be forwarded or not, a node counts how many transactions r_n(t) signed by n has been received in the last W seconds. In accordance to the formula given by Eq. (1), the node forwards the transaction if the following condition is satisfied:
d_n\geq d_0 + \left\lfloor{\gamma\cdot r_n(t)}\right\rfloor
Due to the asynchronous nature of the system, some of the transactions may be received in burst, invalidating the previous formula. We consider a correcting term c>0 which allows to accept transactions with lower difficulty. This parameter is known by all nodes. We modify the previous formula into:
d_n\geq \max\{d_0; \ d_0 + \left\lfloor{\gamma\cdot r_n(t) - c}\right\rfloor\}
Sybil protection
With node identities involved, the protocol requires a Sybil protection mechanism to discourage counterfeit identities. The Sybil protection mechanism proposed for Coordicide is a stake-based reputation system, called mana, and will be discussed in detail in a different post. In the adaptive PoW approach, in order to adapt the node throughput to its reputation, a node has to modify its base difficulty d_0 according to its mana. Hence, in practice, the parameter d_0(m_i) is inversely proportional to the node reputation m_i.
Simulations
Setup
We build a Python simulator with Jupyter notebook in order to verify whether the adaptive PoW algorithm can mitigate the problems described in the introduction. In these simulations, we consider a simple scenario with a single node to evaluate the maximum throughput it can generate.
Suppose a node has computational capability \mu measured in number of operations per second. We assume a node can belong to one of the following three categories depending on its computational power:
- IoT, where \mu = 10^{-1}\times 10^6;
- Laptop, where \mu = 10^{0}\times 10^6;
- FPGA, where \mu = 10^{6}\times 10^6.
Furthermore, we assume that the number of operations needed to solve PoW at difficulty 14 is a random variable uniformly distributed with mean 3^{14}~\approx~5\times 10^{6}. Hence, a IoT device will be able to solve it with an average time of 1 minute.
Finally, we set the following global parameters:
- Base difficulty d_0 = 10;
- Adaptation rate \gamma = 0.1, which means the node increases the PoW difficulty every 10 transactions sent within the time window;
- Time window W = 1000 s.
In the following subsection, we present the simulation results when a node wants to issue 5000 transactions in the shortest possible time, i.e., we aim to maximize the total throughput.
Results
- Fixed PoW
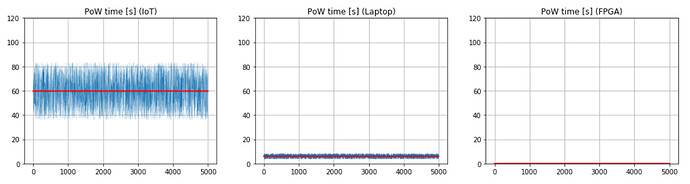
In this subsection, we present the simulations results based on the current fixed PoW algorithm, i.e., when \gamma = 0. In Fig. 1, we show the time (in seconds) needed to compute the PoW for IoT, laptop and FPGA. The red line shows the average time needed to compute the PoW. As we expect, IoT devices require on average 1 minute for a PoW difficulty of 14. Laptops improve this time to about 6 seconds, while FPGAs run 6 orders of magnitude faster than laptops (i.e., they solve the PoW in a few microseconds).
Figure 1. Time (in seconds) needed to compute fixed PoW (difficulty = 14). The red line shows the average PoW time.
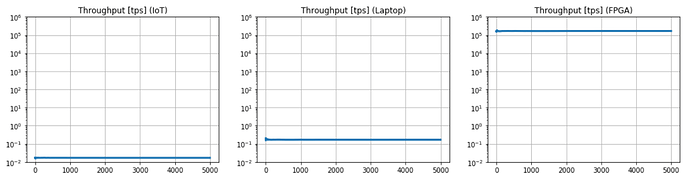
According to these numbers, in Fig. 2 we show the throughput generated by the nodes, computed as the number of transactions per second. In the current IOTA implementation, the usage of FPGAs can speed up the computation of several orders of magnitude, preventing low-power nodes to access the network successfully and enabling spam attacks.
Figure 2. Throughput (in transactions per second) with fixed PoW (difficulty = 14).
- Adaptive PoW
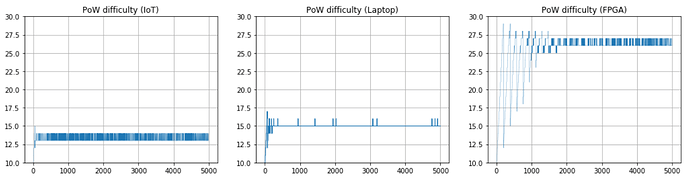
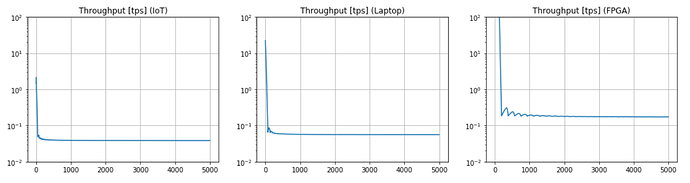
In this section, we analyze the adaptive PoW algorithm. In Fig. 3 we show how the PoW difficulty changes over time. In particular, we see an initial transient phase where the difficulty progressively increases. Then, the difficulty oscillates around a certain value, which depends on the computational capabilities of the device: for instance, IoT devices are able to solve a PoW with difficulty 14, while FPGAs can solve up to a difficulty of 27.
Figure 3. PoW difficulty variation over time.
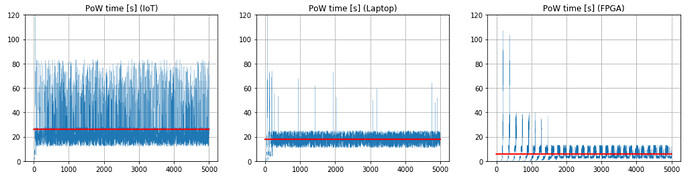
Such a different difficulty mitigates the gap between the solution time for the PoW between the different devices: while IoT can solve the puzzle faster than in the fixed scenario, high power devices see their PoW time raising considerably. This is the key principle behind the adaptive PoW algorithm: make life easy to IoT devices (which is one of the most important IOTA use cases), while bound the power of FPGAs and ASICs (Fig. 4).
Figure 4. Time (in seconds) needed to compute adaptive PoW. The red line shows the average PoW time.
In fact, it is interesting to see that specialized hardware cannot spam indefinitely the network or create congestion, because its allowed throughput is capped in the same order of magnitude of low-power devices. Figure 5 shows this fundamental result, which proves the validity of the proposed approach.
Figure 5. Throughput (in transactions per second) with adaptive PoW.
- \gamma parameter tuning
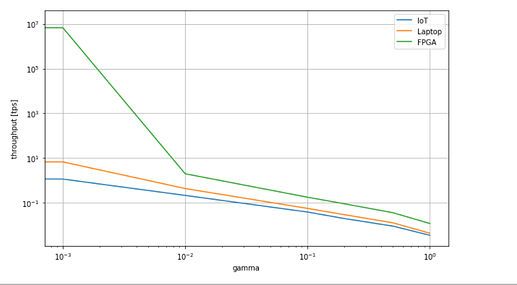
In this subsection, we investigate how to initialize the adaption rate parameter \gamma. In Fig. 6, we plot the throughput generated by the three class of nodes according to different values of the \gamma parameter. Note that the plot is in logarithmic scale. Interestingly, for 10^{-2}\leq\gamma\leq 10^{0} the gap between the throughput generated by the different devices is kept under the same order of magnitude. A better understanding about this parameter should also consider the time window W. This last point is left as a future work.
Figure 6. Throughput for different values of \gamma parameter (logarithmic scale).
Future work
- Analyze how the algorithm works in a multi-node network topology through simulations;
- Analyze how the consensus on \textit{mana} is relevant for the correct functioning of the protocol;
- Explicit the function that computes the algorithm parameters (e.g., base difficulty d_0) according to the node reputation.
Bibliography
[vigneri2019] L. Vigneri et al., Achieving Fairness in the Tangle through an Adaptive Rate Control Algorithm, IEEE ICBC, 2019.