/*** This work is being carried on with the collaboration of @Vidal and @vassil ***/
Preliminaries
Motivation
In the current implementation of IOTA, nodes are allowed to issue new transactions after solving a cryptographic puzzle. This mechanism aims to deal with spam attacks. However, due to the intrinsic parallelizable nature of the function used for the puzzle, an attacker may rent specialized hardware (e.g., FPGAs) in order to speed up such a computation (in the order of several orders of magnitude), and successfully spam the network. In this article, we propose an alternative function, called verifiable delay function (VDF), which is not parallelizable. For a complete description of the motivation leading to this article, we remind the interested reader to the post "Adaptive Proof of Work’’.
State of the art
VDFs has been recently formalized by Boneh et al. [Boneh2018]. These functions can only be solved in a predefined sequential number of steps (i.e., the difficulty, set as input parameter) which cannot be parallelized. However, its verification time is small. Furthermore, theory guarantees that an adversary has, in practice, no chances to find a correct solution randomly.
In both Proof of Work (PoW) and VDF a node has to perform some computation to solve a given puzzle. We list here the key differences between the two approaches:
- VDFs are mainly based on iterative computation of a function (e.g., iterative squaring in RSA groups, points addition in elliptic curves), and thus they cannot be parallelized.
- A VDF is a deterministic functions while PoW is based on probabilistic hashing. Hence, faster hardware will always compute VDFs faster than users with general purpose computers, which can lead to monopoly in a potential race.
Various researchers have proposed different VDFs based on specific number-theoretic functions, e.g., modular exponentiation [Dwork1993, Pietrzak2018, Wesolowski2019], supersingular isogenies over elliptic curves [Defeo2019], pairings over elliptic curves, injective rational maps between extensions of finite fields [Boneh2018]. In the following, we propose a implementation of VDF for the Tangle based on the work of Wesolowski [Wesolowski2019].
A VDF for the Tangle
Goal
In this article, we propose an alternative implementation, based on VDFs, to set a maximum allowed throughput per node. Our goal is to limit the transaction rate to guarantee spam prevention such that the access to the network is only proportional to the mana (a discussion about mana is provided in a different post, called "Mana comparison’’.) owned, and not to the processing power.
Set up
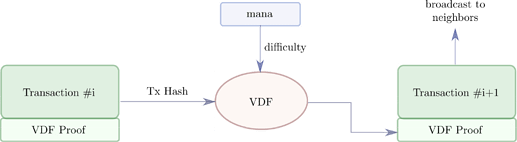
The main building blocks of our proposed anti-spam mechanism are depicted in Figure 1. When a node wants to issue a new transaction, it must solve a VDF that takes two input parameters: (i) the transaction hash of the previous transaction h issued by the same node; (ii) a difficulty parameter d, that depends on the mana owned by the node, indicating the number of iterations to compute. The solver, then, will attach to the new transaction a proof of the computation of the VDF. Thanks to this proof, when the transaction is gossiped, all nodes can verify in short time whether the solution of the VDF is correct.
Figure 1. Building blocks of our proposed VDF-based anti-spam mechanism. The function considered takes as an input the transaction hash of the previous transaction and a difficulty, and produces a valid proof.
VDF based on modular exponentiation
The function used as a VDF must satisfy the following three requirements:
- Fairness: every node in the network must be able to solve a specific VDF in similar time, i.e., for a specific number mana must correspond a specific throughput.
- Verification time*: each node must be able to verify fast that the VDF has been solved correctly. We target a verification time in the order of 10^{-4} seconds.
- Output size: the size of the VDF-related information attached to the transaction must be small, because the bandwidth available during the communication between nodes is limited.
In order to deal with the previous requirements, we choose a VDF based on modular exponentiation, which guarantees fast verification time. In particular, we take inspiration from [Wesolowski2019] to reduce the size of the proof. Furthermore, we want to mention that the fairness requirement listed above is satisfied by modular exponentiation in the sense that specialized hardware can gain, at most, one order of magnitude, while PoW can introduce discrepancies of more than seven orders of magnitude.
As anticipated, we choose a function based on modular exponentiation, where the solver must compute x such that x = h^{2^{2^t}}\mod N, where N is a modulus of size \lambda bit known by all nodes in the network. The parameter N = p\cdot q is the product of two large primes, as in the RSA public key scheme. A main challenge is to generate N in a distributed way such that none of the participants can guess the values of p or q. To this end, we are currently developing an algorithm based on the previous work of Boneh and Franklin [Boneh2001] and Fredriksen et al. [Frederiksen2018].
After the computation of the VDF, the solver calculates a proof of its solution. We decide to forward such a proof instead of the solution itself in order to decrease the verification time. Furthermore, in order to prevent the factorization of the modulus N, which would break the protocol, we require \lambda to be at least 1024 bit. On the other hand, a 128-bit proof provides enough security at the cost of little overhead (i.e., the transaction size will increase by only 16 bytes).
Performance evaluation
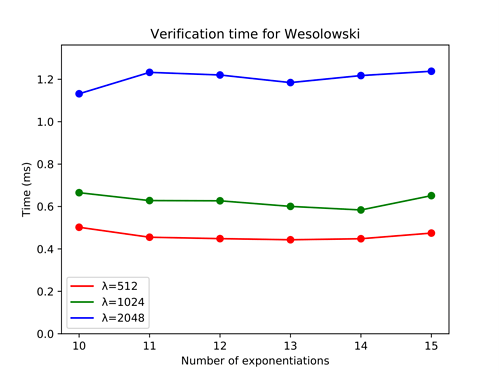
We built a C++ simulator using the NTL library to evaluate the verification time when the proposed VDF is used. In Figure 2, we plot the verification time when the modulus N has length \lambda equal to 512, 1024 or 2048 bit. We vary the difficulty t of the VDF between 10 and 15. First, we note that the verification time only depends on the modulus length, and not on the number of iterations. This result is not valid for other VDFs [Pietrzak2018]. Second, the time needed to compute the verification does not exceed 1.2 ms even though we consider large modulus, e.g., N=2048. Furthermore, while using the NTL library already provides an acceptable verification time, the GMP library or even hardware implementation may probably lead to better performance.
Figure 2. Verification time for Wesolowski’s VDFs in C++
Future work
The research on VDF will follow three main directions:
- Provide a secure and efficient algorithm to create the modulus N in a decentralized way.
- Speed up the verification time both by using a more efficient implementation (e.g., GMP) and some mathematical tricks (e.g., pre-computation).
- Define more rigorously the integration into the IOTA protocol.
Bibliography
[Boneh2018] D. Boneh et al., “Verifiable Delay Functions”, in Lecture notes in Computer Science, 2018
[Boneh2001] D. Boneh and M. Franklin, “Efficient generation of shared RSA keys”, in Journal of the ACM, 2001
[Defeo2019] L. Defeo et al., Verifiable Delay Functions from Supersingular Isogenies and Pairings, in Cryptology ePrint Archive, 2019
[Dwork1993] C. Dwork and M. Naor, “Pricing via Processing or Combatting Junk Mail”, in Advances in Cryptology, 1993
[Frederiksen2018] T. K. Frederiksen et al., “Fast Distributed RSA Key Generation for Semi-Honest and Malicious Adversaries”, in Advances in Cryptology, 2018
[Pietrzak2018] K. Pietrzak, “Simple Verifiable Delay Functions”, in Innovations in Theoretical Computer Science, 2018
[Wesolowski2019] B. Wesolowski, “Efficient Verifiable Delay Functions”, in Lecture Notes in Computer Science, 2019