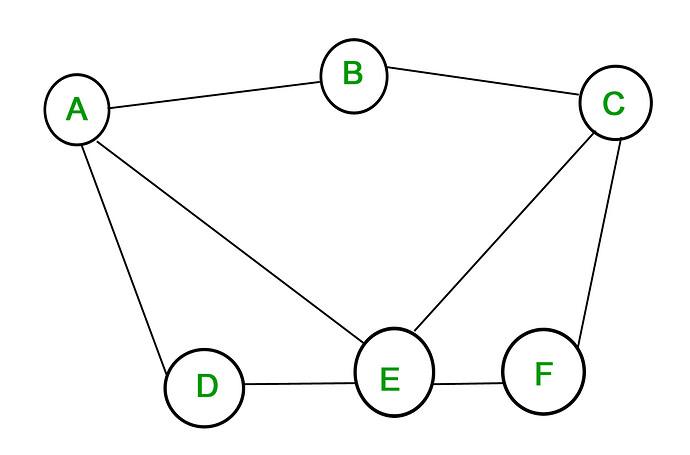
Hans has devised his reality based ledger state calculations which is very useful and interesting. However, partly due to reattachments, the structures created are complex and hard to visualize. This makes algorithms difficult to analyze and verify.
In this note, we present a mathematical tool called simplicial complexes to visualize realities. Besides providing good theoretically terminology, simplicial complexes can perhaps also optimize the underlying algorithms.
This note is a summary, and I omit the technical details in order to be more readable. I am preparing a the technical document with all these details.
I touched on some of these topics at the research summit in Barcelona, but I am not sure if anyone remembers!
Simplicial Complexes
A simplex is the a geometric shape made by joining together some vertices. There is a simplex for each dimension.

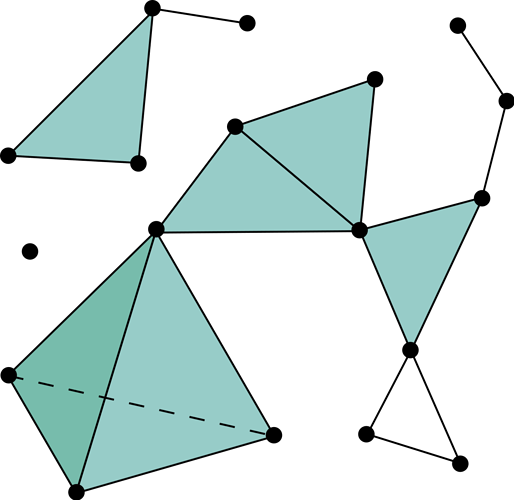
As demonstrated in this picture, the 0-simplex is a point, the 1-simplex is a line segment, the 2-simplex is a triangle, and the 3-simplex is a tetrahedron (note that this shape is “filled in”). The 4-simplex is the 4 dimension analogue of a tetrahedron and is not pictured here. The 0-simplex has 1 vertex, the 1-simplex has 2 vertices (the end points), and so on.
Simplices (plural of simplex) have faces: in fact each subset of vertices determines a face, and each face is also a simplex. The faces of a 1-simplex are the end point vertices. Tetrahedrons have 4 triangular faces. Also, an entire simplex is itself a face. In our terminology, faces can be of any dimension. The empty set is also always considered a face (and is the “-1 simplex”).
If you glue several simplices together along their faces, you get a simplicial complex. The simplices of a Simplicial complex are its faces.
A graph is a simplicial complex.
Each edge is a 1-simplex, and the the graph is formed by joining these 1-simplices along their vertices, i.e. their faces. The faces of this complex are just the edges and vertices.
The following are higher dimensional examples.
Simplicial complexes are used in many places. In pure mathematics, they are used in combinatorics and algebraic topology. Since any triangulated surface is a simplicial complex, they are used heavily used in computer animation software. Simplicial complexes also can also described the relations between clusters of firing neurons in the brain.
Conflicts
Let $V$ denote the value tangle. Let $K$ be the set of conflicting transactions. Let $\Delta(K)$ be the nonconflicting subsets of $K$. We can construct a simplicial complex whose vertex set is $K$ and whose faces correspond to $\Delta(K)$. If $X\subset K$ has not conflicts, and $Y\subset X$, then $Y$ is conflict free too, and thus each conflict free set defines a simplex. Moreover, we can simply think of $\Delta(K)$ itself as a simplicial complex and refer to each conflict free set as a “face”.
Every face $F\in \Delta(K)$ defines a reality: every reality is contains a nonconfictling subset of $K$. Specifically, let $R_F\subset V$ be the largest downset of the value tangle whose payloads form a solidified UTXO graph not containing $K\setminus F$. Then $R_F$ is the reality corresponding to $F$.
Thus all the realities are indexed by the faces of $\Delta(K)$, and $F\subset G$ means that $R_F\subset R_G$.
For example, consider $K={x_1,x_2,y_1,y_2}$ with two conflicting pairs ${x_1,x_2}$ and ${y_1,y_2}$. Then $\Delta(K)$ is the square:

The face ${x_1,y_1}$ corresponds to the reality that accepts $x_1$ and $y_1$ and rejects $x_2$ and $y_2$. The face $y_2$ corresponds to the reality which accepts $y_2$ and rejects $y_1$ and both $x_i$.
The resulting poset of realities is the face poset of $\Delta(K)$.

The point here is that the square is much easier to visualize and understand then this messy poset.
Lastly, note that $K$ can contain other transactions that are not conflicts. For example, suppose a transaction $z$ is contained in a message with a questionable timestamp. Then we can add $z$ to $K$ resulting in the simplicial complex

with four triangles corresponding to the realities defined by ${x_i,y_j,z}$.
Validity and reality membership
I claim that simplicial complexes can provide can simplify some of the algorithms, at least maybe from the human perspective. We give two examples, the first is about validity.
To simplify what I write here, let us just assume for a moment that reattachments are forbidden (the following can be made to work with reattachments, but it would take more words to describe).
In this case, each value object $v$ has a minimum reality containing it. This reality corresponds to the intersection of all the realities/faces containing it. Let $F_v$ be the face corresponding to this reality.
For example, in the scenario described above, suppose that $F_v={x_1}$. Then we know that realities containing $v$ correspond to the faces ${x_1},{x_1,y_1},{x_1,y_2}$. Thus, we encode all the realities memberships in one face.
We can use the faces $F_v$ to easily determine validity and can be inductively maintained. Suppose a new value object $v$ arrives which does not contain a conflict. Suppose $v$ references $u_1,\dots,u_n$ (including UTXO references). Let $F$ be the “closure” (aka join) of faces $F_{u_1},\dots,F_{u_n}$. Then $v$ is valid, if and only if $F$ is a face. Moreover, if $v$ is valid, then $F_v=F$. This works because $v$ is contained in the intersection of all the realities of that each $F_{u_i}$ is contained. This set is empty precisely if $F$ is a face or not, and if $F$ is a face, then it is the minimal face in this intersection.
The faces $F_v$ are also easy to maintain when adding conflicts or snapshotting away conflicts, although we omit the algorithms here.
Monotonicity
Each conflict is voted upon, and so each vertex has the label 0,?,1 with 0 and 1 denoting dislike and like, and ? denoting pending. Each face then takes the least opinion of all its vertices. Thus, if a vertex is disliked, then all the faces/realities containing it can be flagged as disliked too. Similarly, a reality/face is not liked until all of its vertices are liked.
If the voting works correctly, all the liked vertices should belong to a single face. As time goes on, we can prune the disliked faces off of our simplicial complex.
Moreover, we can deduce the liked status of any value object $v\in V$ via is the same as the face $F_v$. In particular, $v$ is disliked if $F_v$ has a a disliked vertex, and is liked if and only if all the vertices are liked.
Conclusion
There is more I can write about, and I may make a second post with more detailed algorithms However, I hope my main point is clear: simplicial complexes provide a good language for talking about realities.
I would appreciate your feed back, particularly if you all feel that these ideas are useful.