In this topic, I review one known solution for the reachability problem. This problem appears in different forms across our algorithms. The solution was originally proposed for static graphs, but can be modified in a straightforward way to our settings.
Notation: Given a DAG $G=(V,E)$ and two vertices $x,y\in V$, we write $x\le_{G} y$ if there exists a directed path from $y$ to $x$. A past cone of $x$ is the set ${y: y\le_G x}$. A subset $C\subseteq V$ is called a chain if the elements of $C={x_1,\ldots,x_s}$ have linear ordering, i.e., $x_1\le_{G}x_2\le_{G}\ldots \le_{G} x_{s}$.
Reachability problem: For two vertices $x,y\in V$, check whether $x\le_{G} y$ (using a minimal number of operations)
In the following, we associate $V$ with a proper subset of integers. Consider the following DAG.
Chain decomposition: A partition $V_1\sqcup V_2 \sqcup \ldots \sqcup V_k=V$ is called a chain decomposition if for every $i\in[k]$, elements in $V_i$ form a chain.
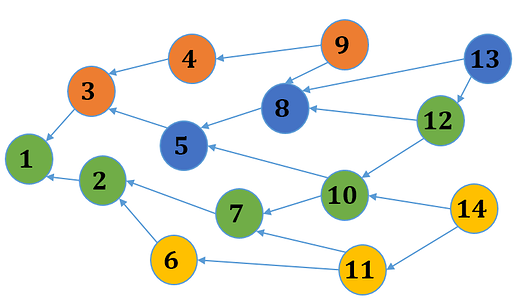
Suppose some chain decomposition $V_1\sqcup V_2 \sqcup \ldots \sqcup V_k$ is fixed. Each vertex $x\in V$ belongs to the only chain $\mathbf{chainID}(x)={i: x\in V_i}$ and has the rank within this chain $\mathbf{rank}(x)=|{y\in V_{\mathbf{chainID}(j)}: y\le_{G} x}|$. For instance, the above DAG can be decomposed in the following way.
Past rank vector: For a vertex $x\in V$, define $\mathbf{v}^{(x)}$ to be the vector of length $k$ whose $j$-th coordinate shows the rank of the closest vertex in the $j$-th chain, i.e.
$$
\mathbf{v}^{(x)}j =
\begin{cases}
\min\limits{y\in V_j, \ y\le_{G} x} \mathbf{rank}(y),\quad &\text{if }\exists y\in V_j \text{ s.t. } y\le_G x \
*,\quad &\text{otherwise}
\end{cases}
$$
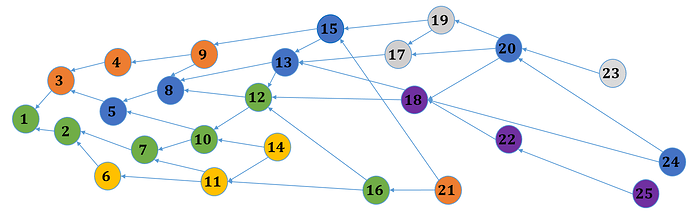
The concept of past rank vectors can be illustrated using the above example.

Clearly, to solve the reachability problem for vertices $x,y\in V$, one can simply compare two values $\mathbf{v}^{(x)}{\mathbf{chainID}(x)}$ and $\mathbf{v}^{(y)}{\mathbf{chainID}(x)}$.
Now review some basic properties of this approach.
Space complexity: $O(k|V|)$. As an optimization, we might store only integers (and no $$) in our vectors. Then, if a new chain is created at some point, there is no need to update the past rank vectors for old vertices.
Time complexity: $O(1)$. If we don’t store $$, then it can be $O(\log k)$.
Suppose that new vertices are attached to old vertices with in-degree 0. Then probabilistic and deterministic algorithms for updating chains are possible.
Clearly, the optimal number of chains is equal to the width of the DAG. Under some good assumptions on the distribution of new vertices, it seems possible to obtain descent upper bounds on the number of chains when the chain decomposition is updated in a randomized way (something like: with high probability $1-\epsilon$, the number of chains is bounded above by $f(\epsilon)$ * the width of a DAG).
Suppose a new vertex $y$ is attached to vertices $x_1,\ldots,x_p$ and $y$ is assigned to chain $t$, i.e., $V_t\gets V_t \cup {y}$. Then the $j$-th coordinate of the past rank vector $\mathbf{v}^{(y)}$ is computed as
$$
\mathbf{v}^{(y)}j =
\begin{cases}
\max\limits{l\in[p]} \mathbf{v}^{(x_{l})}j,\quad &\text{if }j\neq t,\
|V{t}|, &\text{if }j=t.
\end{cases}
$$
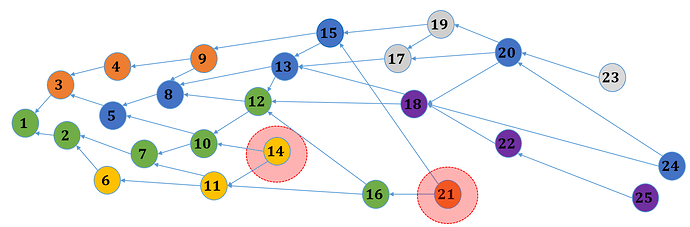
Main issue: This approach might be problematic when the width of a DAG is large. More specifically, when the past cone of new vertices contain too many chains.
In this example, the yellow chain is not reachable from all new vertices 23,24,25, so it might be a good idea to not store $*$ in the past rank vectors of new vertices. The orange one is reachable, but can not be updated, so we can try to rescue it (by removing 21 from the orange chain).
The discussed approach has some similarity with marker sequences. It has a shorter running time (for marker sequences, one needs to traverse the marker DAG), but requires more space to store the data structure (for marker sequence, we store only the ranks of the closest markers).