Introduction
In Coordicide it is planned to employ a tip selection (TS) algorithm called Restricted Uniform Random TS (RURTS). In this algorithm, parents are only selected from a subset of tips that have no greater timestamp difference to the issued tx than \Delta. This introduces the possibility that txs pass this window without obtaining an approving tx, thus becoming orphaned. We must ensure that the likelihood of this event happening becomes very small. This must be true also in an adversarial environment where a malicious node could attempt to increase the orphanage. For example by spaming txs that don’t contribute to the growth of the tangle in any meaningful way the malicious node could achieve that honest nodes’ txs can be distracted from advancing the tangle and which can in turn lead to orphanage.
Assumptions
Txs are not considered as valid tips on arrivial, rather they have to go through a waiting period c before being considered as valid tips. This rule is because the like status of a tx is not yet decided. E.g. for FPC we can set the like status of a tx to dislike if another conflicting tx is discovered within the window c. Furthermore this means that the all-familiar delay h (=network delay+PoW+etc) in our known models for the tangle is now replaced by c and for the remainder of this blog we will think in terms of the time unit c.
Analysis in the honest environment
Simulation results show that we expect an approximately exponential dependency to - k \Delta where k is the number of parents a tx selects. Increasing either can decrease the orphanage significantly.
The orphanage attack
This attack has similarity to the blowball attack where an adversary manages to obtain a large proportion of the tx issuance bandwith. It should be noted that compared to pre-coordicide where the issuance rate is determined purely by the amount of PoW invested, in Coordicide a scenario where the attacker obtains a large bandwith proportion is less feasible. This is because the adversary is required to either possess sufficient active access mana or has to hope that the network is strongly underutilized for at least a time of the order Delta. Nevertheless, in times of strong underutilization in the network an adversary may obtain a bandwith proportion close to 1.
A node issues txs, with proportion q of the network capacity, that approve only txs from the same node. Furthermore from its own txs it approves only those where the timestamp is most close to the end of the window Delta. The latter step maximises the number of spammed tips. Note: It is not important whether those txs are already approved or not since if q is sufficiently large the node can just select the oldest non-approved tx and if the flood of tips is too large the oldest non-approved tx will get closer towards the age Delta as the attack continues. So for simplicity a laziness check is of no importance here.
Simulation results show that there is a critical point around (1-q)k=1 where an adversary would always be successful in causing a high orphanage rate, independent of how large Delta is selected (however the high q must also be maintained as long as Delta). Beyond this point an exponential dependency of the orphanage rate to approximately -k(1-q)\Delta is expected.
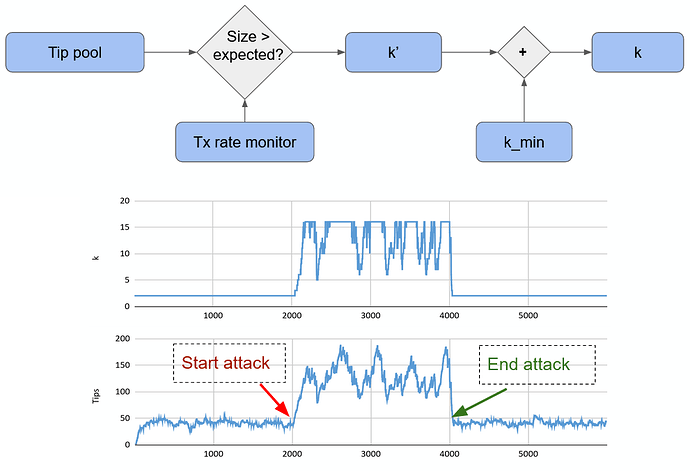
It is important to note that this type of attack can be easily be identified by a quickly increasing tip pool size.
Mitigation strategy 1: increase k permanently
From a protocol point of view increasing the number of parents to for example k=8 seems feasible without decreasing the performance or increasing the tx size noticeable. Furthermore, continuing the example for k=8 would require that the adversary has at least 80% of the tx issuance capacity. Although a step in the right direction, 80% in an underutilized network may be feasible and thus this approach alone may not be sufficient. Nevertheless it has the nice feature of decreasing the time to reach high confirmation confidence.
Mitigation strategy 2: decreasing q
The node software may be shipped with a control that dynamically increases the tx issuance rate to a certain proportion of their allowance in times of an attack. More precisely nodes can compare the current tip pool size to the one they would expect from the tx issuance rate. From this difference each node can increase its (empty data) tx issuance rate, effectively decreasing q. This is a particularly effective approach if q is very close to 1 but the active access mana of the adversary is not that large.
Mitigation strategy 3: increase k dynamically
Similarly to the honest spamming control, node software may also be shipped with a control for dynamically adopting the number of parents. Since the orphanage rate is driven by something like (1-q)k this is particularly effective if the normal k, i.e. the one in an honest scenario, is low. From a different point of view this approach maximises performance under honest conditions (faster TS, lower tx size). While during times of increased tip pool size or an orphanage attack the network switches into a safe mode with minimally increased tx size.