In this thread I want to discuss an idea of a new voting scheme which might be superior to our current approach (CA/FPC) and which builds upon Leslie Lamports ideas around building a 99% attack resistant system.
It would have the following benefits:
- easier to implement (hopefully)
- 99% attack resistance against the amount of “hashing power” or “bad nodes”
- no “external” attack vectors (like the network topology)
- nodes can never “fall out of sync”
- resilient against large scale network splits
- no need for reattachments and promotions ever (tps == ctps)
- much smaller message overhead for the voting
- new ways to distribute “mana” through collaborative tx issuing (maybe possible to create a more fair and even distribution of mana?)
- could 100% be used in the IoT realm (in contrast to FPC)
We have discussed the initial ideas in the last weeks already but due to the lack of concrete algorithms or concepts, it was hard to come to any kind of conclusion. We have brainstormed a few different concepts during the research summit but we always found a few points that at least challenged their feasibility.
I think I now have a concrete concept that might not have many (maybe any ![]() ) issues left and I want to use this thread to discuss it with you guys.
) issues left and I want to use this thread to discuss it with you guys.
Before I start explaining the different building blocks, I want to summarize why I think it might be worth exploring this line of thinking by talking about a problem with our current solution.
The Problem
The biggest drawback of our current voting-based coordicide solution is the subjective consensus aspect of it.
In contrast to most blockchains, where the output of the consensus (the “longest” chain) is always “published” to everybody - our consensus is “local”. This means that nodes have no “objective” way to verify that they are indeed still in sync with everybody else in the network.
Instead, they have to rely on an external layer (the voting layer) to secure them from attacks. While our additional protection mechanisms (eclipse-protection.ixi, proof of opinion, random thresholds in FPC and so on …) should make these kind of attacks as “expensive” and hard as possible, it might still happen (at least in theory), that somebody manages to attack this layer which would allow him to make single nodes fall out of sync.
I have previously proposed to add an additional protection mechanism, that makes nodes monitor the accumulated mana in the tangle to bring back some form of objectivity into our solution.
This would allow us to detect things like “eclipse-” or “network-split” attacks by reacting to sudden shifts in the amount of “economic activity”. While this is most probably doable, it is not entirely clear how the exact rules for such a detection would look like (it would at least require some additional research).
The solution: On-tangle voting
The idea of an on-tangle voting is actually not new. The original white paper version of the tangle is essentially an on-tangle voting approach. The amount of votes is measured in the amount of cumulative hashing power that approves a certain transaction and the consensus mechanism is heaviest subtangle (with the most “votes”) wins.
Since using PoW for voting is problematic (hash races), we came up with the concept of mana. We shortly discussed a mana based on-tangle voting but concluded that it would be too “slow” to deal with splits in opinions, so that we would have to abandon too large parts of the tangle in times of attacks.
What if our conclusion was wrong? The basic idea of this proposal is to go back to the white paper version of the tangle and adjust it to work with mana instead of PoW. At the same time we will try to get rid of pretty much all of the problems of the white paper version of the tangle by slightly modifying a few of the key concepts (tip selection, “expensive” cumulative weight calculations, reattachments / promotions …).
Step 1: Polymorphic Transactions
The first real building block of this proposal is something which I call polymorphic transactions.
Currently a transaction in IOTA can only mean one thing: It “approves” two referenced transactions. Since transactions can only express “approval”, the only way to deal with “disapproval” is to abandon the “bad” parts of the tangle.
This is not very beneficial for an on-tangle voting mechanism because the outcome of the voting is not clear upfront (as the word “voting” implies). We would therefore have to abandon large parts of the tangle, if nodes would issue transactions that are not immediately in line with the majority opinion. This would increase the need for reattachments and would allow an attacker to harm the network - even if a double spend would ultimately not be successful. We therefore need to find a way for nodes to express their opinion in transactions without having to be worried about them being abandoned later on.
To achieve this, we change the perception of a transaction to “like” instead of “approve” its referenced parents (branch / trunk). Furthermore, to be able to express disapproval, we introduce an additional flag in the metadata of every transaction - the branch dislike switch - which changes the meaning of the referenced branch transaction in the following way:

Step 2: Local modifier based initial opinion
To determine the initial opinion of a node, we use a similar local modifier based rule as in our current coordicide solution:
A node “likes” a transaction if it is not conflicting with another transaction that it has seen before.
Note: We do not wait like in our current approach because having an additional “undecided” option just makes the voting harder.
Step 3: New Tip Selection Algorithm
In the white paper version of the tangle, the tip selection algorithm was a very crucial part of the consensus because it had to “count” the votes (find the heaviest subtangle) before being able to hand out the tips for attachments. This counting of votes was an extremely heavy operation because it required us to do a random walk and therefore created a massive bottleneck for the scalability of the protocol.
In this new proposal, I want to decouple the tip selection and the consensus which allows us to build a much simpler and much more robust algorithm that can not be gamed by attacking the structure of the tangle.
The only purpose of the new tip selection algorithm is to allow nodes to efficiently select tips that are reflecting their current opinion.
It works like this:
- We maintain two lists of tips: “liked” and “disliked”.
- We select the trunk uniformly at random from the list of liked tips.
If the list of disliked tips is empty:
- We choose the branch also from the list of “liked tips”.
- We set the branch dislike switch to 0 - the transaction likes both of the referenced transactions.
If the list of disliked tips is not empty:
- We choose the branch from the list of “disliked tips”.
- We set the branch dislike switch to 1 - the transaction only likes the trunk.
As soon as a transaction arrives, that is in line with our own opinion (likes a transaction that we like and/or dislikes a transaction that we dislike):
- We remove the referenced transactions from their corresponding tips list and add the new transactions to our list of liked tips.
As soon as a transaction arrives, that is NOT in line with our own opinion (likes a transaction that we dislike and/or dislikes a transaction that we like):
- We add the new transaction to our list of disliked tips.
This simple algorithm allows nodes to express their current opinion in a very efficient way without having to do any random walks.
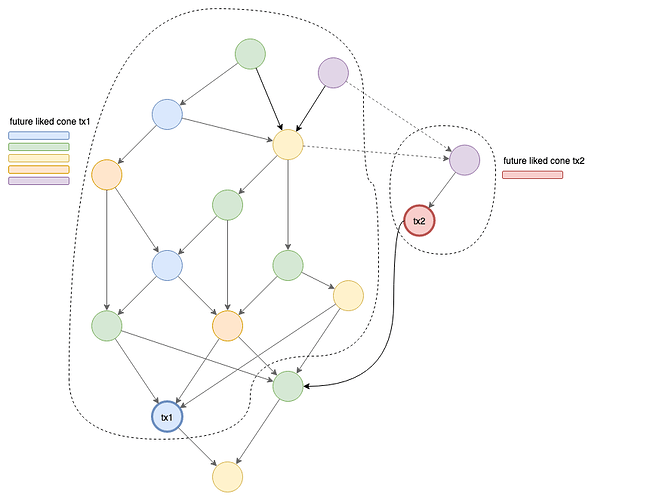
Step 4: The "future liked cone"
In our current perception of the tangle, we already have the concept of the future cone of a transaction, which describes all of the transactions that directly or indirectly approve a certain transaction.
Following this idea, we define the “future liked cone” (FLC) to contain all of the transaction that directly or indirectly “like” a transaction.
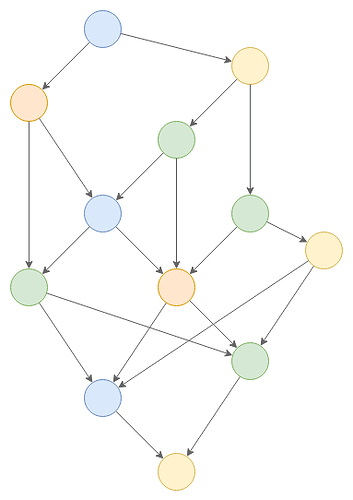
To understand what this means, I want to show a short example how a double spend would look like using the mechanisms described so far. We start with a “healthy tangle” that doesn’t contain any conflicts:
Since none of the transactions are conflicting, all of the transactions “like” both of their referenced transactions (solid line).
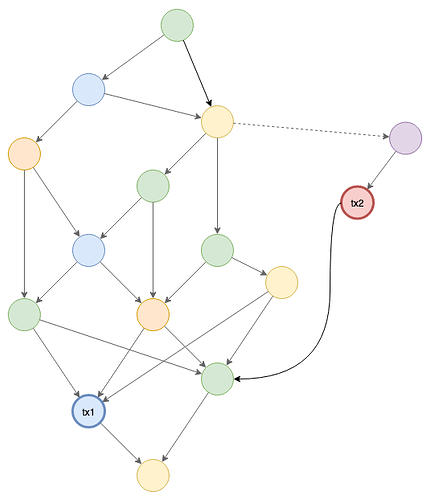
As soon as a double spend arrives, it is set to disliked by the nodes that have already accepted the first transaction and gets referenced by their tip selection algorithm accordingly (dashed line):
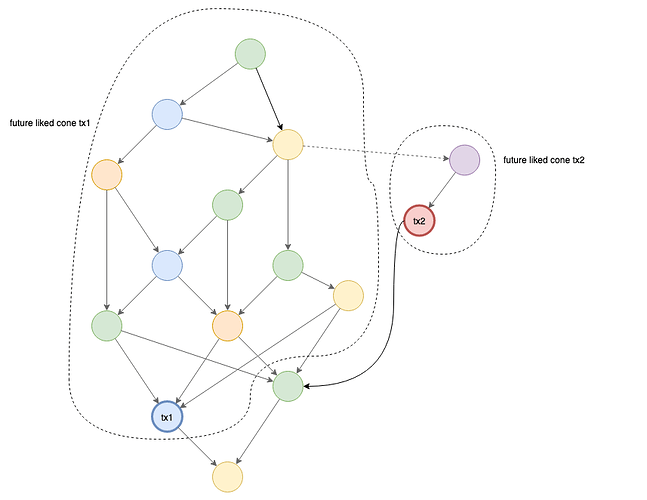
The future liked cone can now be determined by following only the “liked” references (solid arrows):
The concept of the FLC will play an important role in the following building blocks.
Step 5: Parallel "realities"
Instead of trying to maintain only a single “global” version of the ledger, we keep track of all the parallel versions that are introduced by conflicting transactions as well. These different realities coexist next to each other and all the transactions in the FLC of one of the conflicting transactions prefer this reality over others.
n conflicting transactions introduce n + 1 different realities:
-
the realities that like one of the n conflicting transactions
-
the reality that doesn’t like any of the n conflicting transactions (kill all)
All transactions that are trying to spend the same input are part of the same conflict set. Nodes can by definition only like exactly one option out of the n + 1 possibilities of a conflict set.
Realities are organized in a hierarchical way. We start with a “master reality”, which contains all of the currently liked transactions. Every disliked conflicting transaction creates a “sub-reality”, which inherits all of the balances of the master-reality but differs in its perception of the balances affected by the conflicting transaction (and their dependencies - transactions that spend the double spent funds further). A UTXO model would be extremely helpful from an algorithmic point of view, because it allows us to exactly “follow the stream of funds” and construct the parallel reality with just a few operations (vs having to roll back the whole ledger).
Organizing the ledger in such a hierarchical way has multiple benefits:
-
We don’t have to “copy” the ledger state which is shared between realities.
-
Realities can recursively form sub-realities if the FLC of a conflicting transaction contains additional conflicts.
-
To retrieve the balance of a reality, we simply need to recursively ask our parent realities until we find a reality that contains funds on the requested address.
Two non-conflicting realities (of different conflict sets) can merge into another aggregated sub-reality.
To keep track of which transactions belong to which reality, we can implement a simple algorithm:
-
On arrival of the conflict:
-
We create the conflicting reality by calculating the differences in the ledger state (by following the UTXO stream of funds).
-
We walk through the FLC of the conflicting transaction (which should be very short at the time of its solidification) and add the identifier of the newly created reality to a list of realities, that this transaction reflects.
-
Whenever a transaction becomes solid that “likes” one of these “marked transactions”, it inherits the union of the lists of realities of its referenced transactions.
Note that we only need to perform this operation for the disliked realities (the ones that most probably became solid much later). The liked realities are already reflected by the “master reality” and we don’t need additional “reality identifiers” inside of transactions to reflect this opinion .
Step 6: Cumulative weight (based on mana)
Our last new concept before talking about the actual consensus rules is the mana based cumulative weight which will allow us to decide between conflicting realities.
In contrast to the white paper version we however don’t need the cumulative weight of every single transaction - we only need to calculate the cumulative weight of the reality as a whole (represented by its FLC).
To do that, we simply walk through its FLC and make a unique list of all the nodes that it contains. The accumulated mana of the nodes in this list is the “cumulative weight” of this reality.
Note: In fact, we don’t even have to walk the tangle for this, since we can already maintain this unique list of nodes while transactions are being attached to this reality (on arrival / solidification).
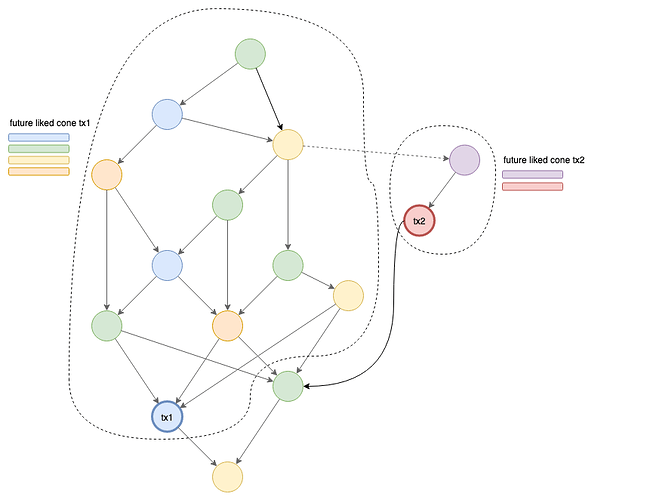
Let’s look at the earlier example and let’s compare the cumulative weight of the two FLCs (every node is represented by a different color):
Note: The FLC of tx1 contains more nodes (and potentially more mana) than the FLC of tx2.
Step 6: Numbered transactions and changing opinions
So far we have defined, how nodes can cast votes (TSA) and how we can count the votes (cumulative weight), but to reach consensus, we need to allow nodes to change their opinion.
The basic idea is that later votes will replace earlier votes if they express a different opinion.
We therefore need to be able to tell which vote was the later one (preferably without doing an “expensive” random walk). An easy and straight forward way to do this is by making nodes include an ever increasing nonce as a transaction counter in their transactions. They start with a counter value of 0 and increase it whenever they issue a transaction.
Note: This per-node-transaction-counter is also beneficial for the rate control and spam protection (see specs of the rate control we talked about on the research summit).
Whenever we receive a transaction that likes a different reality of the same conflict set. we remove it from the unique list of “supporters” from the old reality and instead add it to the unique list of “supporters” from the new reality - this way the weight of realities can change (and in combination with the consensus rules tip to one majority opinion).
Step 7: Consensus rule - the heaviest reality wins
Now we only need to define when and how a nodes changes its opinion (the actual consensus mechanism).
The consensus rule is very simple: The heaviest reality wins. For sub-realities: If no reality is heavier than any other reality, we decide based on the hashes of the transactions that created the sub-realities.
As soon as a sub-reality has more weight than the main reality, we adjust our opinion and follow the now heavier reality. We do this in the following way:
-
We first calculate the new state of the master reality by rolling back its conflicting transactions followed by applying its sub-reality specific changes. Then we create a new sub-reality for the previous master reality, that contains the rolled back changes.
-
We add all of our liked tips to the list of disliked tips.
-
We walk through the FLC of the new master reality and if a disliked tip is contained in there, we add it to the list of liked tips.
-
Then we continue issuing tips as normal.
Note: We can again maintain separate list for liked tips for every sub-reality on arrival to save the random walk.
Nodes are only allowed to switch their opinions if the newly stated opinion references more accumulated mana in its FLC than the previous one. Nodes that violate this protocol will immediately loose all of their mana and therefore their influence in the voting. See the following example of “referenced mana” of a FLC.

Let’s look at our previous example of a conflict in the tangle and see how nodes change their opinion:
The purple node (that initially favored tx2), now adjusted its opinion to follow the heavier reality and attached his new transaction accordingly. Since its later vote replaces the earlier one, it is now counted towards the acumulated mana of the other FLC.
Since every node follows the same behavior, the algorithm tips extremely fast. As soon as one transaction is slightly favored, the whole network will instantly follow suit with its next transactions. Most of the times, the difference in mana of the issuing nodes of the conflicting transactions themselves might already be a big enough tie breaker for the tipping to happen.
Even in situations where the tipping takes a bit longer, it only affects the consensus of the balance of this particular conflict since non-conflicting transactions become part of the “master reality” anyway.
Step 8: Faster decisions - collaborative transaction issuing
To be able to make “fast” decisions and reach a fast finality, we need to have big mana holders constantly cast votes. Since forcing them to issue transactions would create a lot of unnecessary overhead for these nodes, we need to find a different way for them to publish their opinion.
One of the ideas was a collaborative transaction issuing process, where nodes that want to issue a transaction first ask a big mana holder for their opinion and then include its answer in the transaction. This way every transaction has two voters (the issuer and a big mana holder) and we receive votes of enough mana relatively fast (more TPS means faster confirmations).
The mana of the the collaboratively issued transaction is shared among the issuing nodes (to create an incentive to answer these kind of requests).
Step 9: Elders - making the algorithms more efficient
To make the algorithms more efficient and to not have to keep track of all existing nodes when calculating the cumulative weight, we define a subset of the k highest mana nodes to be the “elders”.
If we have a fixed amount of elders, then the “set operations” and mana calculations can be performed by “ORing” a bitmask of k bits. These operations are highly efficient and first tests show that such a mechanism could process double-digit millions of TPS (50 million TPS in the first benchmark).
Summary
I want to summarize this new approach by looking at a visualization of the two approaches:
-
The old approach which shows abandoned parts and their corresponding reattachments.
-
The new approach that shows the FLCs (bold black lines) that also get abandoned but kept in the tangle through their dislike references (dashed line).

The old approach completely abandons disliked parts and forces users to reattach their transactions. The new approach will also make more and more nodes abandon their previously favored sub-realities for the heavier reality (here the “master reality”) but the “abandoned” realities will stay in the tangle via their"dislike references" (dashed line).