This document outlines a proposal for a ‘deterministic gossip’ algorithm which can be tuned to give the desired trade-off between redundancy and efficiency. Existing proposals for gossip/epidemic/anti-entropy algorithms are typically probabilistic, and hence only provide probabilistic guarantees of dissemination of blocks. This algorithm is deterministic and hence offers guaranteed delivery of blocks under the assumption that the network topology does not change and nodes follow the protocol. In the case of changes in topology, node misbehaviour or connectivity issues, the partial ordering provided by the DAG can be used to detect failures and recover missing blocks through solidification requests.
Protocol Outline
In a standard flooding setting, nodes send every block to all of their neighbours, and as such every node receives every block from every neighbour, and all but the very first copy of the block are discarded, resulting in high redundancy. This redundancy can be good, as it offers robustness in the case of faulty or malicious neighbours, but it also represents a significant inefficiency which can surely be improved upon. In what follows, we propose a deterministic gossip algorithm which attempts to balance redundancy and efficiency in a precise manner by exploiting the assumption that the topology of the network remains more or less constant.
In what follows we refer to blocks issued by a node a as a-blocks. The protocol proposed here is based on the idea that for each node i in the network, one neighbour of node j \neq i will deliver all i-blocks to node j before any of the other neighbours of j, on average. In other words, one neighbour of j will have a shorter path from i than any of the others and will hence deliver i-blocks sooner.
The idea is that we start with a flooding algorithm, and each node j calculates which of its neighbours is expected to deliver i-blocks \forall i \neq j first, i.e., which neighbour has the shortest path to node i. Node j can then instruct all other neighbours to stop sending i-blocks to them. When a node j instructs its neighbour n to stop sending it i-blocks, we say that node j i-prunes its neighbour n. This can be modified to include some redundancy and hence robustness by allowing the top k neighbours to send i-blocks for each i. We call this k-redundant. For example, node j accepting i-blocks from its top 3 neighbours (ranked by shortest path from i to j) would be 3-redundant and the original example with only the best neighbour can be referred to as 1-redundant. We will mostly focus on the 1-redundant case, unless otherwise specified, which can be easily generalised to k-redundant.
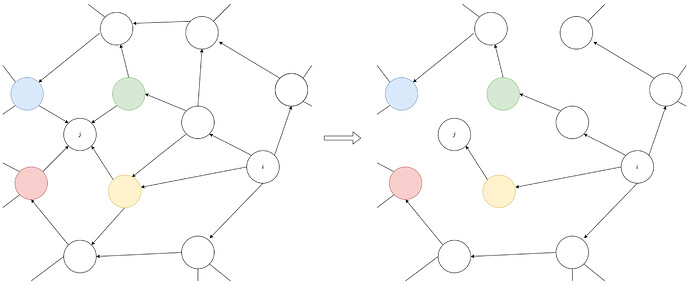
When every node has i-pruned all but one of its neighbours (the neighbours with the shortest path from i), the flow of i-blocks through the network graph forms a tree rooted at node i. The below figure shows the flow of i-blocks in the network under a flooding algorithm, and then shows the flow of i-blocks after all nodes have i-pruned their neighbours according to a 1-redundant algorithm.
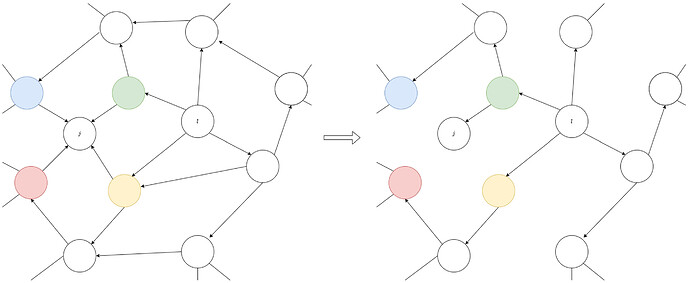
The next figure shows the same as above but for l-blocks. There is an equivalent tree rooted at each node m in the network corresponding to the flow of m-blocks. In the cases shown in these figures, we can see that node j will receive all i-blocks from the yellow neighbour, while it receives all l blocks from the green neighbour.
Some Security Considerations
By removing redundancy in blocks, we leave nodes somewhat more vulnerable. In the case of flooding, eclipse attacks require an adversary to control all neighbours of the node being attacked, but in the case of a gossip protocol with less redundancy, the node responsible for delivering i-blocks to node j can potentially single-handedly i-eclipse node j, i.e., censor the flow of i-blocks reaching node j. Equivalently, in the k-redundant case, the attacker would need to control as little as k specific neighbour to i-eclipse node j.
The problem of i-eclipsing may be partially solved by the DAG structure of the ledger, that is, if j receives a block c which is a child of an i-block, before that i-block is received from the designated neighbour responsible for forwarding i-blocks, then the neighbour that forwarded block c should be sent a solidification request for the missing i-block, and this neighbour should immediately be designated responsible for delivering i-blocks to j.