OT*'s implications on tips and more
With the introduction of the new modular consensus mechanism based on OT-FPCS, and the removal of FCOB, management of tips based on only weak and strong parents might become impractical mainly out of the following reasons:
- Prone to blow up: If branches are undecided for too long, the weak tip pool might blow up and message orphanage increase since every message needs to be picked up individually without AW propagation to its past cone.
- Inefficient and too complicated: Tracking weak tips requires the node to constantly evaluate its opinion regarding its liked branches. Only then a weak tip pool can be built. If the opinion switches, also all weak tips need to be removed that are part of the now liked branch. Conversely, all messages that are in a new disliked branch need to be added to the weak tip pool.
- Lazy evaluation of opinion: Without the weak tip requirement all nodes can simply function as a replicated state machine. The opinion can be evaluated only when needed, i.e., on tip selection, because that is the only time a node casts a vote. To keep an implementation efficient, it might still be beneficial to cache the opinion.
This document introduces a new proposal called dislike switch and its implications on current components such as branches, markers and tip selection.
Dislike switch
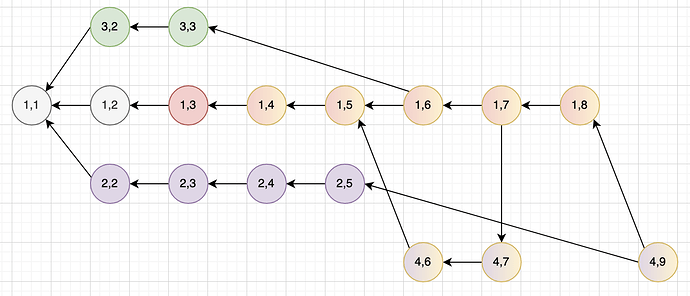
The general idea is straightforward: We allow nodes to specify which transactions they don’t like in the past cone of a selected tip. Additionally to the disliked transaction, the node needs to reference the liked message out of the conflict set with a special liked reference (just approving the message’s payload but not its past cone) if it is not in the selected tip’s past cone. The following figure shows the mechanism in more detail.

Message 13 approves messages 5 and 11. It dislikes D and likes C (in past cone, hence no like reference necessary) and dislikes A, and, thus, needs to reference B's message with a like. Therefore, the branch of message 13 results in an aggregated branch of purple+yellow. Message 14 does inherit the branches of message 13, thus, it does not support transactions A and D (and their corresponding branches red and green).
Message 17 approves messages 11 and 16 but dislikes B. Consequently, it inherits the aggregated branch of red+yellow. A direct reference (like reference) to message 4 is not needed because it is in its past cone.
Branches
As depicted in the figure above, messages can be in the future cone of a conflict but not be part of the branch itself through specific exclusion/dislike of the corresponding transaction, and thus branch.
As soon as the overall branch is determined (currently implemented rules still apply) it can be booked and AW for the message’s branches tracked accordingly. The way we track supporters and calculate the AW for branches does not need to be changed.
The requirement of referencing the liked transaction’s message adds some complexity and is restricted by max parents age but makes sure that a message always belongs to a branch. Otherwise, it might be possible to dislike everything in the past cone, effectively freeing a message from all its branches, and, hence, making a message again part of the master branch.
The like reference should help to speed up voting as more nodes actively express their opinion on their liked branches. Additionally, by receiving such a message all nodes can solidify the conflicting transactions and create the corresponding branches in their local ledger and tangle.
Markers
Markers are an abstraction layer of the tangle that help to infer structural information about it. As such, there’s no inherent concept of conflicts and conflict branches when looking at them. Therefore, they can be used with the dislike switch as we simply need to inherit supporters to all the past cone except the disliked transaction.
Approval weight propagation

Approval weight approximation and propagation with the dislike switch can stay mostly as is described here.
In the example above, the message with marker 4,6 adds support to the purple and yellow branch as described previously. Its weight in terms of markers is propagated according to its strong parents down to lower markers in its own sequence (in this case none exist), and to all referenced sequences i.e., sequence 1, starting from 1,5 down to 1,1. The like reference does not propagate weight with respect to markers but only adds support to the branch.
Similarly, when booking message with marker 4,7 it adds support to all markers smaller than and equal to 4,7 including the referenced sequence 1, starting from 1,5 down to 1,1.
When a marker gets confirmed, we need to walk in its past cone and confirm every message and transaction individually until we reach other confirmed messages. At this time, the dislike switch needs to be taken into account. Specifically, the intersection of the marker supporters and the branch supporters (in case there is a branch as a result of a conflicting transaction) has to be used to calculate the weight of individual transactions, and only if the confirmation threshold is reached, a message/transaction can be confirmed.
Sequence continuation
In sequence 4, marker 4,7 is parallel to the two messages between 2,5 and 4,9 which is why these messages can not get a marker. However, due to the workings of the dislike switch, the message with marker 4,7 might not be a tip anymore but another sequence continues (as is the case with 1,7 and 1,8). With the marker 4,9 a new marker in sequence 4 can be created because of the references between sequences (sequence DAG), and we can easily deduce that 4,7 is in the past cone of 4,9 while booking the message.
Branch mapping
To efficiently map a part of the tangle to a branch we, rely on the mapping between branches and marker sequences. This means, that also with the dislike switch, we need to establish this mapping of sequences to branches.

The figure above shows how this naturally happens, e.g., message with marker 1,6. The message inherits the branches from its parent 1,5. It does, however, not inherit the branch from 3,3 as it dislikes D. Therefore, it is in sequence 1 which is mapped to the aggregated branch red+yellow starting from 1,4.
Let’s consider 4,6 as another example. It inherits the aggregated branch red+yellow from its parent. Because of the like reference to B the message obtains the purple branch, and dislikes the red branch, through which it creates a new aggregated branch purple+yellow. Consequently, a new sequence is started and mapped to the branch.

In the above example a new conflict (blue) arrives and everything in the future cone of marker 4,6 needs to be updated to reflect the branch change. All messages in sequence 4 that have marker 4,6 in their past cone (e.g. as past marker) are implicitly updated through just changing the mapping of 4,6 to the aggregated branch purple+yellow+blue. The sequence DAG links 4,7 and 1,7, which enables updating 1,7 explicitly and, thus, everything in its future cone implicitily.
Tip selection
Tip selection becomes simple. The tangle as such has only one tip set (previously known as strong tips) and for a node it does not matter in which branch these tips reside. The node, therefore, can keep track of tips easily without the need of knowing its own opinion constantly. Only after selecting tips the node needs to establish the messages’ branches, set the dislike switch, and possibly add the liked references accordingly. Also the selection itself can simply be *URTS on the tip set.
Remarks and questions
Dislikes overflow
Let us assume that the maximal number of dislike switch used in one message is 64.
In this way TSA should avoid picking a set of tips that have more than 64 disliked messages in their past cones.
However, this situation may not always be possible. For instance, an attacker could issue 65 transactions and wait until there is a transaction txVictim whose past cone contains all these 65 transactions. The attacker then, issues 65 double spends, making it possibly impossible to use txVictim as a tip. Possible solutions are to rescue txVictim as a weak parent or demand to reattach txVictim.
Weak parents (lightweight version)
As mentioned in Dislikes overflow it might be necessary to still support weak parents to rescue individual messages. The same might be true for timestamp voting. However, for these type of weak parents no separate tip pool needs to be kept and the weak reference can be set on demand. In fact, the described like reference of the dislike switch can in practice be modeled with a weak parent without any additional changes.
Summary
The dislike switch is a simple mechanism that makes it possible to propagate AW to all messages/transactions except the disliked ones, and, thus, solves the aforementioned orphanage problem of only using strong and weak parents. It also allows to evaluate a node’s opinion lazily, and gets rid of inefficient weak tip pools. Furthermore, it speeds up voting decisions through special direct references to liked transactions.
On the other hand, the dislike switch has the limitation of only being valid within max parents age (due to the reference to the liked transaction of the conflict). It adds additional complexity to the protocol, and through it messages can be in the future cone of a conflict but not be part of the branch itself. Furthermore, it can create inefficiencies with the marker sequences if certain structures are kept alive and references between sequences are frequent.
From the perspective of the current implementation of GoShimmer, not too many changes are necessary. First of all the dislike switch needs to be added to the message layout and evaluated when booking. The AW for branches and markers can be tracked as they are now. Only when confirming messages/transactions, it needs to be checked whether individual transactions were disliked by nodes, and might not get confirmed. The tip manager can be simplified to accomodate only one tip set.