Introduction
I would like to thank toothless and Sissors for their help and feedback for this post.
Before the Tangle Multiverse can be used for a consensus method in Iota’s Tangle, it’s necessarily to solve whether an attacker can balance two, or multiple conflicting transactions for prolonged time and harm the network. We call this scenario a metastability.
This post aims to demonstrate that if the Tangle Multiverse would be applied to an environment where every voter share the same perception of voting weights, it would be possible to get rid of the metastability problem with few small additions to the base protocol.
The post became a bit lengthy, but the basic idea can be summarized in the following way: We begin with a strong attacker that has a perfect perception of the network and a perfect ability to time its own moves. The attacker can balance (n) conflicting transactions and keep them in balance as long as he wants. First we introduce a method that uses a modification of Tangle Multiverse in order to push the metastability of (n) conflicting transactions into a metastability of a single transaction (between confirmed or not confirmed).
Next we make an assumption that voters have a shared perception of voting weights, and use that to define unambiguously a single transaction in the history of the Tangle DAG. We examine the direction the metastability was tilting based on the past cone of the defined transaction, and finally use that to break the single transaction metastability. To assume that voters have a shared perception of voting weights might sound quite unrealistic, if we consider the Tangle Multiverse applied to Iota 2.0. Yet, in the discussion part of this post, I give some arguments on why it might actually be a reasonable assumption for Iota 3.0.
Phase 1 — towards a single transaction metastability
Because our approach is partially based on an attempt to measure something unambigiously from the Tangle DAG history, we need to specify certain tools:
Subjective timestamps: (Definition copied from: Objective mana based on “local clocks”)
- Every node includes a timestamp in his transaction that defines when this transaction claims to be issued.
- The timestamp of a transaction needs to be bigger than the timestamps of both of its referenced transactions.
- Honest nodes only use transactions in their tip selection algorithm that have their timestamp set to a value that is smaller than their local time.
The main chain:
This approach assumes that the Tangle DAG forms a “main chain”, which an attacker cannot split into multiple small chains. Yet, the attacker can create side chains that are smaller by their total voting weight than the main chain.
An α-transaction
When a transaction is broadcasted to the network, somewhere at the future cone of the broadcasted transaction other transactions begin to have so many transactions in their past cone that reference the broadcasted transaction, that the senders of these transactions have a majority of the total voting power. α-transaction is a transaction that meets this criteria and has the lowest time stamp. It can be used to proof that the majority of voting weight have “seen” the transaction.
- Note that when defining an α-transaction, we don’t examine parallel reality ledger state, just transactions and their references.
The picture here demostrates this:
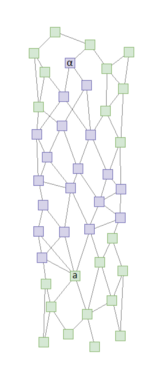
The above picture shows an α-transaction for a transaction a. The combined voting weight of issuers of blue transactions is over 50% of total voting weight of the network.
The α-rule
Because timestamps are gameable, without any additional rules α-transaction is also gameable. An attacker could easily create a transaction(s) with a forged timestamps and send it to the network in a way that only part of the network would see it in time and choose it as the α-transaction. This way different nodes would end up with a different α-transactions.
The picture below shows our approach to prevent this attack:
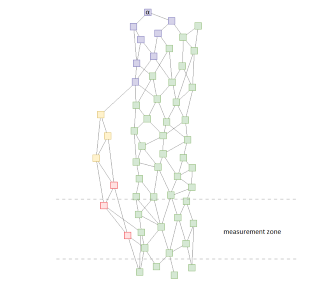
In this picture we have a main chain (green and blue) and a side chain (yellow and red). Lets assume that a node tries to find an α-transaction for a certain transaction and that it would be somewhere in the measurement zone. An attacker has built the side chain afterwards, and tries to interfere with the measurement with it.
Blue transactions are transactions that reference the side chain. A node can differentiate side chain transactions that could interfere with the measurement, by examining the α-transaction of these side chain transactions.
If the difference of timestamps between a certain transaction and its α-transaction is too large, a node wont use it in its measurements.
A transaction meets the α-rule if: the timestamp of its α-transaction subtracted by the timestamp of the transaction, is smaller than (k).
Please note that α-rule cannot differentiate side chains from the main chain. It only aims to prevent an attacker from interfering with the measurement of a certain transaction that is deep in the history of the DAG with forged timestamps.
k is set in a way that almost always a transaction with a timestamp set correctly would meet the α-rule
If an α-transaction is determined by applying α-rule, every honest node should arrive to the same transaction if:
- the examined time period is deep enough in the Tangle DAG history so the Tangle DAG had time to stabilize
- and the honest node had received transactions related to the measurement.
An honest node could rather easily determine, if he had not received the all the necessarily transactions, because he would have an “incomplete” Tangle DAG from that period.
A tip selection counter attack
One method an attacker could still try, in order to interfere with the α-transaction selection, would be to link transactions in a way that by making a single transaction meet the α-rule, it would make the next transaction meet the α-rule, and so on. Finally, the cascade would interfere with the α-transaction selection with the transaction an attacker is targeting at. Luckily it is rather easy for honest voters to detect and prevent this kind of attack with an additional tip selection rule.
The picture below demonstrates this:

An attacker sends a (transaction a) that could affect to the measurement at the measurement level. The transaction is sent with a forged timestamp, and timed in a way that it almost meets the α-rule, but not exactly. Then he sends another (transaction b) in a way that it could make the (transaction a) meet the α-rule. The (transaction b) is also timed in a way that it just barely misses the α-rule. By sending a (transaction c) with a correct timestamp, an attacker could create a cascade that would cause (transaction a) to meet the α-rule and affect to the measurement.
Honest voters could rather easily notice that by referencin (transaction c), it might affect to (transaction a). Honest voters could thus prevent this attack by deciding not to reference (transaction c) at all, before time k has passed.
The tip selection counter attack rule:
- A voter will not reference a transaction, if it will potentially make a transaction that has not met the α-rule meet the α-rule, and if the transaction that would get affected had a timestamp difference to the referenced transaction larger than f.
The majority of total voting power when deciding an α-transaction
To decide an α-transaction we need to determine which voters we consider to be part of the total voting weight at the time of an α-transaction. This could be a rough approximation of the “real” scenario, as long as every node would end up with the same set of voters.
We could do this by taking the transaction we are considering for an α-transaction (“transaction a” in the example below) and then take every transaction in the ledger that has timestamp between: (transaction a)-j and (transaction a)
j = large enough positive number to get an approximation of the current active voters
The picture below demostrates this:
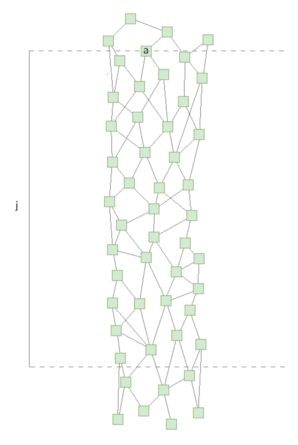
Then we would apply the α-rule to these transactions and finally determine based on this set of transactions the nodes that were sending transaction during this period. These voters would form the total voting weight of the certain moment.
The proposal:
We start with (n) conflicting transactions. When the conflict has been in a metastable state for a certain period of time t(z) based on the nodes local clock, each node determines the time T(0) for the conflict.
T(0) is determined in a following way: We measure α-transaction for each conflicting transaction while applying α-rule to remove possible manipulation of the result. T(0) is the timestamp of an α-transaction with the the smallest timestamp.
From now on we do not need exact measurement points in Phase 1 anymore, so we can use local clocks of different nodes:
T(1) = T(0) + t(a)
t(z) < t(a)
If none of the conflicting transactions gets super majority in T(1) (based on nodes local clocks), honest voters begin to vote for an opinion where none of the conflicting transactions will get confirmed. We call this opinion C.
General voting rules:
- An honest voter will vote for opinion C, if time T(1) has passed based on his local clock and none of the (n) transactions have gained a super majority. The super majority consist from voters that have voted for the transaction whether they have simultaneously voted for opinion C, or not.
- An honest voter that has voted for opinion C will also simultaneously vote for a transaction that he think has the largest portion of voting influence from his perspective.
- An honest voter will pull back his vote for opinion C, if one of transactions gains a super majority and less than 50% of voting influence have voted for opinion C.
- If ≥ 50% of voting influence have voted for opinion C, every honest voter will vote for opinion C.
With these rules the situation can lead into three different states:
- A super majority will vote for a single transaction and none of the honest voters will vote for opinion C.
- A super majority will vote for opinion C.
- There appears a new metastability state where a super majority will vote for a single transaction, but the portion of voters that will vote on opinion C remains in 50%.
When we apply this to the Tangle Multiverse it could look like this:
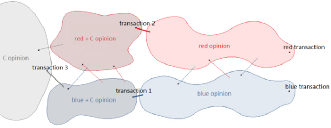
In this demonstartion there are two conflicting transactions (red and blue) and the situation leads to a super majority voting for opinion C.
Red and blue opinion bubbles consist of transactions that vote for the related transactions. Thin lines between these bubbles demonstrate partial likes that tie these two groups together to a single DAG.
As the time T(1) has passed, some voters issues a special transactions (transactions 1 and 2) and state that in addition to voting for a certain side of a conflict they also vote for opinion C.
In this example the transaction 1 would strongly like (thick line) a transaction in the blue opinion bubble and inherit all the opinion realities of the liked transaction. In addition, the transaction 1 would contain extra information that would state the newly added opinion C. The transaction could point this opinion C to the blue transaction by using the hash of the blue transaction. Every transaction that would strongly like the transaction 1, would vote for the blue opinion and opinion C simultaneously.
With this alone we could end up to a situation where the super majority votes for opinion C and the conflict would resolve. Yet, due to Tangle Multiverse voting structures, voters would have to keep jumping between these different colored bubbles for ever if none of the transactions would gain a super majority. Thus, once the super majority is voting for opinion C, honest voters would have to create yet another opinion bubble (C opinion).
A voter/voters could create the C opinion bubble by creating a transaction (transaction 3) that strongly likes any of the different colored bubbles, and in addition states that because the situation is resolved, the transaction would only vote for the opinion C in that conflict. This statement would cancel the vote he had inherited from his strong like conserning the conflicting transactions and the voter would vote only for opinion C. (This extra information could again be directed by again adding the hash of the blue/red transaction as an extra information.) Every voter who strongly likes this type of transactions would only vote for opinion C in that specific conflict.
What would happen to tokens tied to the conflict? If we believe that double-spend attempts shouldn’t happen by accident, we could punish the attacker by permanently freezing these tokens. That would probably be the simplest answer. Alternatively, we would have to find a way to unlock these funds by some method.
Phase 2 — resolving a single transaction metastability
The basic idea of this phase is that after narrowing down the problem to a single transaction metastability, we try to define unambiguously a certain transaction in the history of the metastable conflict. We use that “anchor transaction” as our measurement point, and try to determine which side the metastability was tilting based on the anchor transactions past cone. Because we have a shared perception of voting weights, everyone should end up with the same result.
The proposal:
We use four different moments of time:
- T(0) = the α-transaction with the smallest timestamp when comparing α-transactions for each conflicting transaction while applying α-rule to remove possible manipulation of the result.
- T(1) = T(0) + t(a)
- T(2) = T(0) + t(b)
- T(3) = T(0) + t(c)
t(a)≪t(b)≪t(c)
At time T(3) based on a nodes local clock, every honest node selects the transaction in the Tangle DAG that has timestamp closest, yet still smaller than T(2) and that is not ruled out by the α-rule. We call this transaction the “anchor transaction”.
Because nodes use the past cone of the anchor transaction for their measurements, it would be necessarily to have the anchor transaction link to the main chain in its past cone with a reasonable time period. For this reason every honest node applies yet another rule (the past cone rule) to prevent the attacker from manipulating the measurement.
The past cone rule: The transaction needs to have over 50% of voting weight in its past cone in a way that only transactions with timestamps larger than the timestamp of the examined transaction -t(x) are accepted.
The picture here demostrates this:

In the picture above: the (transaction a) is a part of a sidechain and won’t thus reference over 50% of voting weight during time t(x) in its past cone. The (transaction b) is at the main chain and references over 50% of voting weight in timeperiod of t(x).
If there are multiple transactions with equal timestamp, the node selects the one with a smallest hash. Every honest node should arrive to the same transaction in this manner.
Then we examine the past cone of the anchor transaction and use these transactions to create a “transaction set”.
If, based on the transaction set, less than 50% of voters vote for C in the conflict, every honest voter will begin to pull back their vote for C.
Otherwise, every node will begin to vote for C.
It is worth noticing that between T(2) and T(3) the single transaction metastability situation might have been resolved and the transaction might have been “confirmed“. Yet the transaction might be again rejected after T(3). The receiver of the transaction should not accept a “confirmation” that had happened between T(2) and T(3), before T(3) and some safety marginal had passed.
DDOS-attacks and network splits:
In this approach it is assumed that Phase 1 would have time to end before the Phase 2 would begin. The assumption is that: with Phase 1 being completed we either have a single transaction with a supermajority, or supermajority is voting on opinion C. This might be compromized with DDOS attacks. In that case we might end up to a situation where none of the transaction has a supermajority and less than 50% of voting weight is voting for C, so none of the actions of Phase 2 would happen. The situation would continue to stay in metastability. After DDOS attack the Phase 1 would be completed and the system would either be resolved, or the situation would result into a single transaction metastability.
Also with a DDOS attack the attacker could prevent any recent transaction from meeting the past cone rule during anchor transaction selection, which would lead to voters pulling back their vote for C, even if there would not be a single transaction with a supermajority.
For this reason we probably need additional mechanism:
We might decide that voters will vote for the side chosen in the Phase 2 only for a certain time period based on their local clocks. After this voters would vote the heaviest opinion reality. A new Phase 1 (and eventually Phase 2) would start if there were not a single confirmed transaction after certain period of time after the ending of Phase 2 (based on the nodes local clocks and T(0). This would probably also allow us to keep the partition tolerance. I have not specified these procedures in more detail here.
Additional notes:
We also could try to optimize this approach and remove the Phase 1 completely. This might however cause some edge cases and make the solution harder to analyze.
Discussion
Why it might make sense to assume that voters have a shared perception of voting weights ?
The Tangle Multiverse is a consensus alternative for FPC (Fast probabilistic consensus). As the Tangle Multiverse is at very early research, FPC is a well studied and proved solution. FPC will be sufficient solution for multiple years, so we shouldn’t stick too tightly on methods used in Iota 2.0. The Tangle Multiverse is mainly a consensus candidate for Iota 3.0.
In Iota 3.0 the most important problem that needs to be solved is scalability (or “infinite scalability”). This requires sharding. We could increase scalability by using methods like “hierarchical sharding” (like done in Ethereum Serenity) and combine it with a source of trust that originates from token value (e.g. mana). Yet, these approaches can only increase scalability to a certain point. To achieve a system that could always grow with the adoption, it would be necessarily to make the trust model identity based. More voters would then bring more trust to the system, making it more secure and scalable.
With identity based systems we need a mechanism to determine voting weights of different users. There are two main approaches for that: subjective approach where each voter determines locally who they trust, and an objective approach where there is additional consensus layer for voting weights.
This post assumes that we have an identity based system with an additional consensus layer for voting weights. Thus, every voter have a similar perception of how much voting weight each voter has.
Although the subjective approach seems more natural to humans, it is not very natural for IoT devices. An IoT device manufactorer probably has no idea where his device will finally operate, or who could be its neighbours in its shard. How could a small device compare so many different forms of trust? Or how should it react to a sudden report of a firewall vulnerability of a certain voter node? For IoT devices it should be enough to trust the DLT solution, that would in turn take care of the complex processing of trust. It should be easy plug’n play for small devices. More generally, I see this as a misconseption of the role of DLT.
Unprocessed trust is like mineral or raw data. It is everywhere and it can be used for many things, but as such it is quite useless. Project Alvarium is a good example what it means when raw data is processed, measured and verified in a way that makes it much more useful. Ultimately DLT should do the same for trust. It should be a “global trust processing machine” that takes raw trust from the external world, verifies, measures and processes it in a standardized manner. Finally the sharding solution should distribute trust in a way that serves users and consensus should secure individual transactions with it. I believe this is the best way to build a scalable layer of trust for IoT devices.
If the “global trust processing machine” sounds too futuristic, I have written a blog post series that describes how a global consensus for voting weights of identified voters could be built. It’s so simple that it’s almost boring. ![]()
Thanks for taking the time to read this! Have a good day!